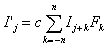, Equation 1
Submitted to Rapid Communications in Mass Spectrometry, August 19, 1996
Sponsor: Werner Ens, University of Manitoba, Winnipeg, Manitoba
Contact the authors by email at beavis@proteometrics.com
Abstract
This paper describes the application of matrix convolution filters to time-of-flight matrix-assisted laser desorption mass spectra to improve the appearance of a particular spectrum and to extract peaks from poorly resolved signals. These filters are commonly used in image enhancement to sharpen blurry images and remove noise because of their general applicability and their modest requirements for calculation speed. The theory of these filters is discussed, as applied to mass spectra and examples of spectra processed using a variety of filters are shown to demonstrate the improvements and artifacts that can be generated.
Mass spectra obtained from time-of-flight mass spectrometers with matrix-assisted laser desorption ion sources have suffered in comparison with other types of mass spectra because of their relatively low resolution and high backgrounds1. In spite of their aesthetic shortcomings, these mass spectra have become the basis of a large number of publications and have become widely accepted in the analytical and biochemical community2,3.
Mass spectra are part of a much larger, general class of data that can be represented as a multidimensional digital array of intensity information. The most studied types of data that fit into this general classification are digital representations of optical images, which are three- dimensional arrays of two spatial coordinates and an intensity. Methods for improving the "quality" and extracting relevant information from blurry, noisy images have become very sophisticated. There are many types of data manipulation used to improve these images. Fourier transformation of the digital data, followed by filtering and inverse transformation can be used to remove many types of noise from images4. Model-dependent transformations can be used to remove predictable defects from images, such as correcting for out-of-focus effects or uniform movement of an element of the image5.
Mass spectra belong to the same general class of mathematical representations as digital images of photographs, except that rather than being three-dimensional arrays {x,y,intensity}, they are two-dimensional arrays consisting of mass-to-charge ratio (m/z) and intensity {m/z,I}. The data to be derived from the mass spectrum is a set of discrete m/z values that represents the m/z values of the ion species produced by the ion source. These m/z values are further processed by identifying the charge of ions and the identity of adduct species, to produce a set of molecular mass data representing the masses of the molecular species present in the original sample.
Some types of data processing have been traditionally applied to mass spectra, such as the subtraction of smooth or curved backgrounds and smoothing using Savitsky-Golay algorithms6. Signals obtained from ion-cyclotron resonance mass spectrometers are only useful after they have been subjected to very intensive image processing using Fourier transforms and related filtering techniques7. The application model-dependent image corrections to quadrupole mass spectra obtained from electrospray ion sources has been exploited commercially using a maximum entropy calculation to determine the best fit for a particular model to the data8,9.
This paper describes the use of matrix convolution filters to time-of-flight mass spectra to improve the appearance of the a particular spectrum and to extract peaks from poorly resolved signals. These filters are commonly used in image enhancement to sharpen blurry images and remove noise because of their general applicability and their modest requirements for calculation speed.
THEORY
A general point that is important to this work is the nomenclature used for the filters that will applied to the data. They are referred to as convolution filters because they take the values of many neighboring points and apply those values to a single point in the enhanced spectrum. This enhancement is performed without any prior knowledge of the general shape of peaks in the spectrum: no basis set of spectral shapes is assumed in the calculation. This situation is very different from a calculation that assumes a basis set of spectral shapes has been transformed by instrumental factors leading to peak broadening or noise, such as maximum entropy deconvolution8,9. Instead, the emphasis in convolution filtering is on a point-by-point (or pixel-by-pixel) enhancement of a new image emphasizing features with a particular property, such as emphasizing quickly varying features (peaks) at the expense of slowly varying features (background). The goal is to emphasize existing features in a spectrum to make the objective assignment of peak centroids easier and to make the presentation of data more illustrative.
Matrix convolution filters were discussed by Savitsky and Golay6 as a prelude to the derivation of their smoothing convolution. It was their impression that matrix convolution filters were less successful at extracting information from their data than the convolution algorithm that they outlined. Matrix-assisted laser desorption/ionization linear time-of-flight (MALDI-TOF) mass spectra present a very different problem than that faced by Savitsky and Golay. Their data set consisted of a series of overlapped peaks with known spectral profiles. The peaks in MALDI-TOF spectra have a sharp component and an associated broad component that produces a hump in the baseline in the vicinity of the peak. The presence of these broad components can significantly degrade the aesthetic quality of a peak, as well as obscure small peaks that occur on the hump. The sharp components of a peak are not easily predicted by theory: their profile is dependent on laser energy, metastable decay rates and instrumental geometry. Matrix convolution filters are appropriate for this type of data, because they only utilize the original data in the spectrum, without reference to an external model of the peak distortions produced by the instrumentation. This "model-independent" nature of matrix convolutions - as well as their speed of calculation - has lead to their popularity in image processing software10.
The general form of a matrix convolution filter for two dimensional mass spectrum information is a simplification of the three dimensional image processing case10. The specific example of a time-of-flight mass spectrum will be used throughout this discussion. A time-of-flight mass spectrum can be represented as an array of intensities Ij, where j represents the time (t) at which the intensity was measured using a simple relationship involving the sampling time (t) of the transient digitizer used, such as t = jt. A convolution filter can be represented as a matrix Fk, where k = -n, -(n-1), …, n-1, n. For the purposes of this discussion, the value n will be referred to as the "order" of a particular filter. This filter acts on a spectrum to produce a new spectrum Ij according to the following expression
, Equation 1
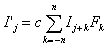
where c is a filter dependent normalization factor
. Equation 2
There are an infinite number of filters that can be generated by altering the values Fk . The filters that are useful for processing mass spectra have two additional properties: they are symmetric (Fi = F-i, i = 0, 1,…, n); and they are of odd order (n = 1, 3, 5,…). These two properties have the net effect of eliminating filters that deliberately shift the position of mass spectral features. Instead, these filters tend to preserve the location of specific features that are being extracted, such as maxima and minima in a spectrum. Using odd order filters allows the convolution to treat the original data point (Ij+0, in Equation 1) as the center of symmetry for the convolution, which is difficult to perform generally for even order filters.
Smoothing and high-pass filters
Two convolution filters are of particular interest for processing time-of-flight mass spectra. The first of these is a smoothing filter, that can be used to reduce high frequency noise in a spectrum. An example of a simple smoothing filter (n = 1) is F = {1,1,1}, c = 1/3. When this filter is used in Equation 1, the effect is to make the intensity at every point an average of the intensity of other points in the neighborhood. Smoothing convolutions of this type are roughly equivalent to Fourier-transform low-pass filters in that they can be used to remove noisy high frequency components from an image.
The second type of convolution filter of general value for time-of-flight spectra is the high-pass filter. An example of a simple high pass filter (n = 1) is F = {-1,3,-1}, c = 1. These filters accentuate maxima and minima, resulting in sharpened peaks in spectra. The value chosen for F0 strongly affects the appearance of the filtered spectrum, a property that will be explored below in the Results section.
Adaptive background correction
A further method commonly used in digital image processing that is of use for improving mass spectra is called "unsharp masking". The name comes from the original, analogue method for performing this type of filtering on photographs10. Digitally, an unsharp mask filter can be expressed as
, Equation 3
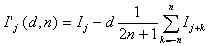
where 0 < d 1. The effect of this type of filter is to remove slowly varying backgrounds from a spectrum, leaving rapidly varying components, such as peaks. The value of n, which is the order of the smoothing filter represented by the second term on the right hand side of Equation 3, determines how wide a feature must be to be removed. The value of d determines the extent to which the filter will remove broad features. The name "unsharp masking" is rooted in darkroom photographic technique and has no intuitive meaning in mass spectrometry, therefore the convolution filter described by Equation 3 will be referred to as "adaptive background correction" (ABC) in this paper.
EXPERIMENTAL
Mass spectrometry
The mass spectra shown below were obtained using a custom-built mass spectrometer constructed at New York University. The instrument was a linear time-of-flight mass spectrometer with a 1 meter flight path and a single field acceleration region. The acceleration potential was +40 kilovolts for all spectra. The flight tube contained a single-wire ion guide, held at -50 volts DC. The detector used was a 25 mm diameter multichannel plate followed by a gridded electron multiplier (both Hamamatsu), configured so that the front face of the channel plate was at ground, with respect to the flight tube.
The matrix-assisted laser desorption ion source used a nitrogen laser (LSI 337ND) as the light source. The laser light was focused onto the end of a 0.20 mm diameter fiber optic (Newport) with a +20 cm focal length lens. The light was transmitted 1.5 meters through the fiber optic. The output end of the fiber optic was imaged onto the matrix deposit in the ion source using a doublet of +20 cm focal length fused silica lenses.
Data analysis
The data acquisition system for this mass spectrometer has been discussed in detail previously11. The system uses a 12-bit, 500 MHz transient recorder developed to improve the dynamic range for measuring matrix-assisted laser desorption mass spectra. Once a spectrum was acquired, it was analyzed using a custom data analysis program called "M/Z". "M/Z" was written in C++ using Microsoft Visual C++ version 2.0. The program was modified to incorporate the convolution filters described above. All data analysis was performed using a 90 megahertz clock speed Pentium-based PC (P90, Dell) running Windows NT 3.51.
Materials
The matrix, -cyano-4-hydroxycinnamic acid, was purchased from Aldrich. The matrix was re-crystallized and extensively washed before use. All solvents were purchased from Fisher, except the formic acid, which was purchased from Aldrich. Matrix solutions were made fresh, just prior to use (see the appropriate figure captions for matrix solvent details). Ribonuclease B and endoprotease Glu-C were purchased from Sigma. The other two samples, human Alzheimer's peptide fraction and chicken liver -N-acetylgalactosaminidase were supplied by the groups indicated in the references as part of ongoing collaborations.
RESULTS AND DISCUSSION
General comments
Considerable experimentation demonstrated that matrix convolution filters could be successfully used to process MALDI-TOF information. This experimentation involved an empirical investigation of the effect of numerous filter matrices on a set of typical MALDI-TOF mass spectra. It was determined that the filter had to be considerably larger than those commonly used in photographic work, where 3x3 or 5x5 filters are usually sufficient. The MALDI-TOF data system used (see the Experimental section) greatly over-sampled the recorded peaks, so it is necessary to use filters of order n = 15 - 25. For convenience, these large filters were constructed using a smaller filter of order n = 5 (i.e., a filter with 11 elements). This smaller filter was expanded into larger filters by repeating elements of the smaller filter. For example, using this process to triple {-1,3,-1} (i.e., an expansion factor x = 3) leads to {-1,-1,-1,3,3,3,-1,-1,-1}. Only odd expansion factors (x = 1,3,5, ...) were used to maintain the symmetry of the filter matrix.
Experimentation also led to the conclusion that simple high pass filters could not be used to process MALDI-TOF spectra. Simple high-pass filters (see the Theory section) produce unacceptable artifacts on spectra, by producing strong undershoots at leading and falling edges of peaks. These undershoots obscured any data near to these edges, resulting in consistent and unacceptable information loss. As an alternative to the simple filter, the following eleven element filter was found to work well on real spectra
, Equation 4
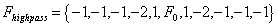
where 10 F0 20. The adjustable parameter F0 determines the behavior of the filter at leading and trailing edges, as will be demonstrated with Figures 2, 4, and 6. This simple filter and its expanded forms, were found to be very effective when applied to poorly resolved peaks.
The spectra shown in the section below all show relatively small mass ranges of much larger mass spectra. The main reason for this choice is the practical difficulty of showing the improvements in the fine details of a peak when displaying a wide mass range. The filters used in this paper can be applied across broad mass ranges simultaneously without producing confusing artifacts.
Examples of filter behavior
The first spectrum used to demonstrate the utility of the convolutions described in the Theory section is shown in Fig. 1 and 2. The sample used to generate the spectrum was ribonuclease B, a small glycoprotein that has a single high-mannose glycosylation with 5 - 9 mannose units.
The effect of adaptive background correction (Eqn. 3) is shown in Fig. 1. The upper trace has no correction, with the base line hump that is characteristic of linear MALDI-TOF protein spectra. The center trace is the same data with a reasonable value of d = 0.6. The hump has been removed to a great extent, giving the impression of improved mass resolution. The measured improvement in full-width, half-maximum (FWHM) resolution was approximately 20%. The lower trace, with d = 1.0, represents an over-correction of the background, although it showed a glycoform with 9 mannose units much more clearly than the other two traces. The effect on the mass of the peaks, determined by calculating peak centroids, was to shift the mass by < 50 ppm. It should be stressed that the convolution filters used to process the data cannot produce any improvements in instrumental resolution: they act by removing broad features and slightly accentuating valleys between peaks.
The effect of using the high-pass filter described in Eqn. 4 is shown in Fig. 2. The upper trace was the same data as shown on the upper trace of Fig. 1. The middle trace used a moderate value for the adjustable parameter F0 = 14, which removed most of the background hump, producing a similar improvement in the perceived resolution of the peaks, while increasing their FWHM resolution by approximately 20%. The lower trace showed the effect of using too small a value for the parameter F0 = 10. This value has clearly produced undershoot artifacts in the spectrum, removing any information about peaks near the rising and falling edges of the two largest peaks. The effect on the mass of the peaks, determined by calculating peak centroids, was to shift the mass by < 20 ppm.
The spectrum used to generate Figs. 3 and 4 was taken using an Alzheimer's peptide fraction that contains considerable C-terminal raggedness, resulting in many peaks separated by the mass of the appropriate amino acid. . The largest signal in the spectrum corresponds to the [1-40] a- peptide13. Alzheimer's disease plaques are very insoluble, so formic acid was used to dissolve the peptides, resulting in formylation peaks that were 28 Da higher mass than the parent peptide signal. These two effects led to a very complicated molecular ion signal, with many of the components poorly resolved. The middle traces of Figs.3 and 4 are clearly resolved allowing masses to be more easily assigned than in the upper traces. The over-corrected bottom trace of Fig. 3 shows the major peaks in the spectrum, but loses some of the smaller formylation signals on the left-hand side of the spectrum. The formylation signals were maintained in the lower trace of Fig. 4, but the undershoot has become unacceptable near the large peaks. The mass assignments for the peaks that were resolved in the upper traces of Figs. 3 and 4 were not affected by the convolution processes.
A more challenging case was used to generate Figs. 5 and 6. The protein, chicken liver -N-acetylgalactosaminidase14, has a molecular mass of approximately 45 kDa, but has N-terminal and C-terminal heterogeneity and several glycoforms. The signal shown in the upper trace of Figs. 5 and 6 has at least four poorly resolved components. It was difficult to objectively assign m/z values to these signals, except for the third signal, which produces a local maximum. Applying ABC to this data (Fig. 5), produces well-defined peaks allowing objective assignment of centroids and hence m/z values. The case with d = 1.0 has been smoothed using a 33 element smoothing filter, to reduce noise. High-pass filtering of the same data (Fig. 6) produces similar results, once again producing four peaks that can be used for obtaining molecular mass information (or evaluating the relative abundance of the four species). The FWHM resolution of the peaks in the lower traces of Figs. 5 and 6 is approximately 200, which is worse than one would expect for a singly-charged ion of mass 15 kDa using this particular instrument.
Figure 7 demonstrates that ABC can be applied over a wide m/z range simultaneously. The same set of parameters was used over a range of approximately 20 kDa, effectively removing the background from the spectrum. Even small, low signal-to-noise features of the spectrum were preserved by the algorithm and the centroids left unchanged to better than 50 ppm. No obvious artifacts have been generated by this process.
CONCLUSIONS
The filters described above have been shown to be of practical utility for objectively finding peaks in matrix-assisted laser desorption/ionization linear time-of-flight mass spectra that were too poorly resolved to be assigned peak centroids and m/z values in the original data. An additional effect of using these filters was a general improvement in the appearance of spectra without significantly altering the expected instrumental mass resolution . It is recommended that when these filters are used to extract features from a spectrum, the enhanced spectrum should be carefully compared with the original data to be sure that no artifacts have been introduced by the filtering process, particularly when using the modified high-pass filter (Eqn. 4).
ACKNOWLEDGEMENTS
The authors would like to thank Dr. E. Castano for his Alzheimer's peptide sample and Dr. A. Zhu for the sample of -N-acetylgalactosaminidase. This work was supported by the Skirball Institute for Biomedical Research at the New York University Medical Center and the Beatrice and Samuel A. Seaver Foundation.
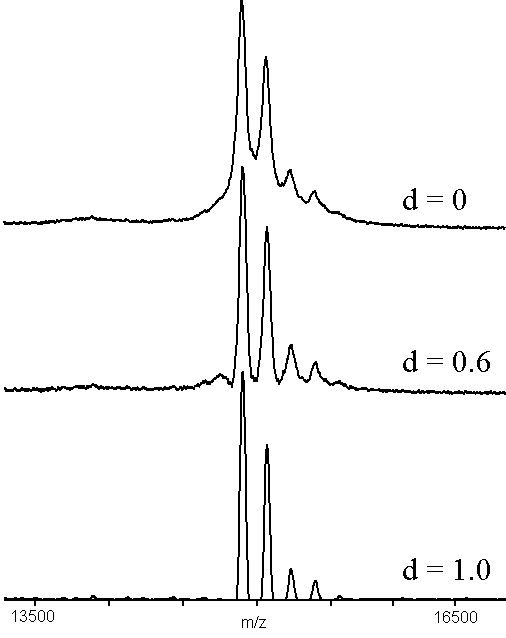
Figure 1. An example of adaptive background correction (n = 55), using a MALDI-TOF mass spectrum of bovine ribonuclease B12 (see text). The sample was prepared by adding 1 microliter of 10 micromolar protein to 10 microliters of matrix solution (2:1 aqueous 0.1%TFA:acetonitrile, saturated with -cyano-4-hydroxycinnamic acid) and mixing. One-half microliter was dried on the sample holder and the results of 100 shots were accumulated.
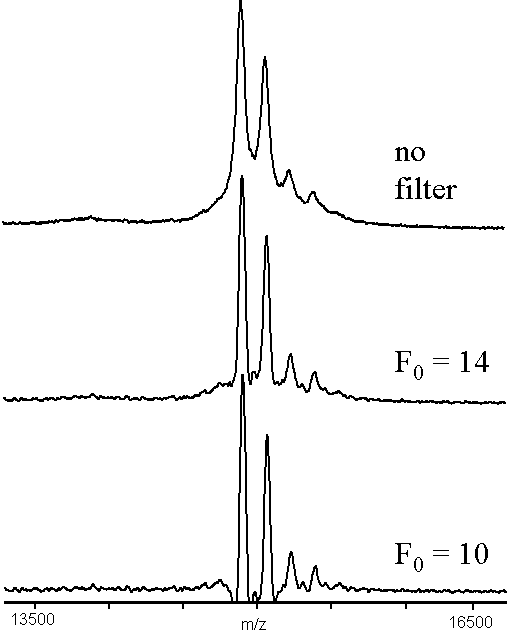
Figure 2. An example of high-pass filtering convolution (x = 7), using a MALDI-TOF mass spectrum of bovine ribonuclease B12. The data used was the same as in Figure 1.
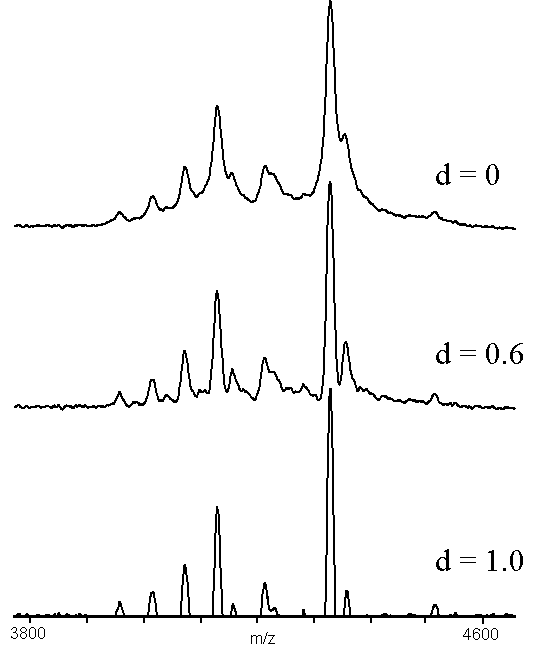
Figure 3. An example of adaptive background correction (n = 30), using a MALDI-TOF mass spectrum of an Alzheimer's peptide fraction13. The sample was prepared by adding 10 microliters of matrix solution (4:4:1 water:2-propanol:formic acid, saturated with -cyano-4-hydroxycinnamic acid) to a tube containing the dried fraction and mixing. One-half microliter was dried on the sample holder and the results of 100 shots were accumulated.
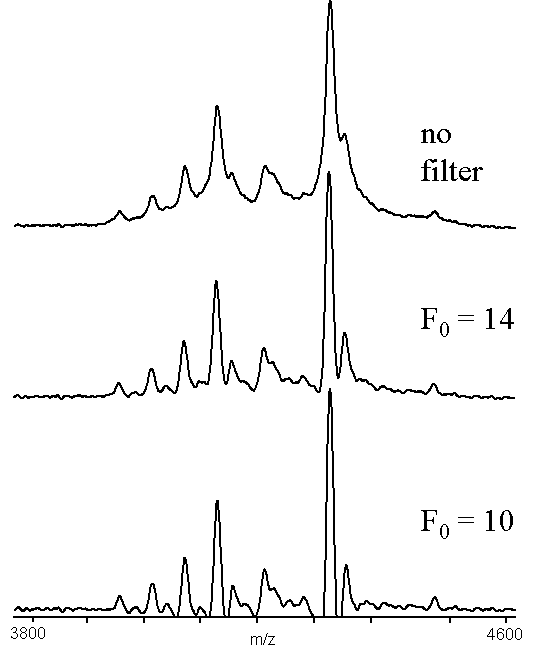
Figure 4. An example of high pass filter convolution (x = 5), using a MALDI-TOF mass spectrum of an Alzheimer's peptide fraction13. The data used was the same as in Figure 3.
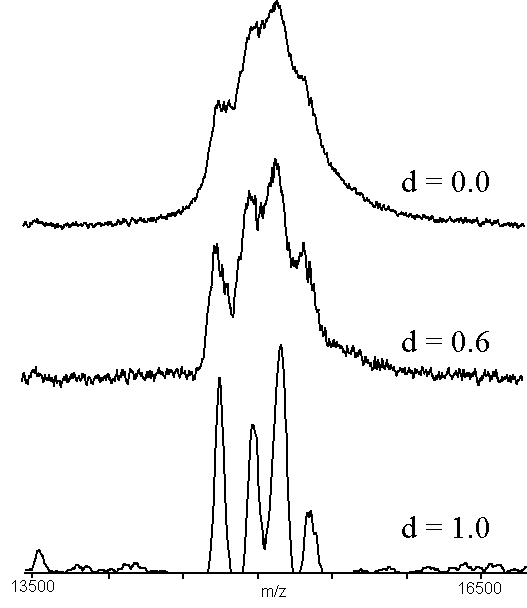
Figure 5. An example of adaptive background correction (n = 55), using a sample of native chicken liver -N-acetylgalactosaminidase14. The sample was prepared by adding 1 microliter of 10 micromolar protein to 10 microliters of matrix solution (2:1 aqueous 0.1%TFA:acetonitrile, saturated with -cyano-4-hydroxycinnamic acid) and mixing. One-half microliter was dried on the sample holder and the results of 100 shots were accumulated. The region shown is the triply-charged molecular ion of the intact protein.
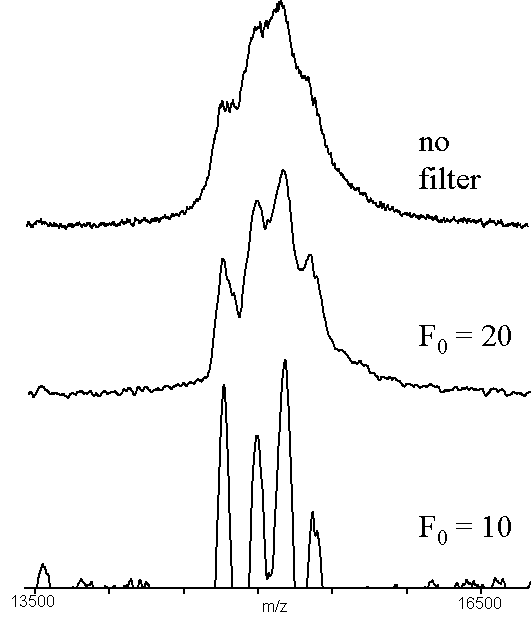
Figure 6. An example of high pass filtering (x = 7), using a sample of native chicken liver -N-acetylgalactosaminidase14. The data used was the same as in Figure 5. The region shown is the triply-charged molecular ion of the intact protein.
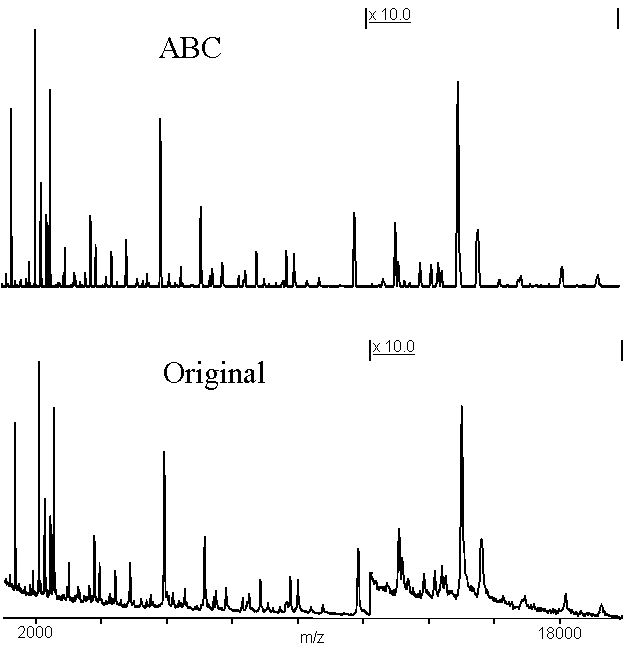
Figure 7. This spectrum shows the mixture of peptides obtained from an overnight autodigestion of endopeptidase Glu-C15. The upper trace is the same data as the lower trace, after applying adaptive background correction (n = 33, d = 1.0). The m/z-axis has been left off the upper trace so as not to occult the portions of the spectrum near the baseline. The right-hand side of the spectrum has been enlarged by a factor of 10 to show small details of the spectrum.
REFERENCES